Transformer Architecture: Understanding Attention Mechanisms and Positional Encoding Techniques

1. Introduction¶

The advent of Transformer models has revolutionized the landscape of natural language processing (NLP) and machine learning, providing state-of-the-art performance on a plethora of tasks, including machine translation, language modeling, and text classification. The Transformer architecture, introduced by Vaswani et al. in the seminal paper "Attention is All You Need", eschews the traditional recurrent and convolutional neural network structures in favor of self-attention mechanisms, thereby enabling the model to capture long-range dependencies and contextual information in a more efficient and effective manner. The vanilla Transformer model, which serves as the foundation for subsequent variants and enhancements, comprises an encoder-decoder architecture that leverages multi-head self-attention and positional encoding to process input sequences in parallel, as opposed to the sequential processing inherent in recurrent neural networks. In this article, we embark on a deep dive into the intricacies of the Transformer architecture, elucidating the attention mechanisms, multi-head self-attention, encoder-decoder structure, and various positional encoding techniques that undergird its efficacy. Furthermore, we explore the latest advancements and future developments in Transformer models, drawing upon cutting-edge research from arXiv and renowned academic institutions.

2. Attention and Self-Attention¶

The attention mechanism constitutes a pivotal component in the Transformer architecture, facilitating the model's ability to selectively focus on specific parts of the input sequence while processing and generating output. The attention mechanism dynamically computes a set of weights, known as attention scores, that quantify the relevance of each input element to the current processing context. These attention scores are subsequently employed to compute a weighted sum of the input elements, thereby producing an attention output that encapsulates the salient information pertinent to the current context.

2.1. Attention Mechanism¶

The attention mechanism can be mathematically formalized as a mapping function that computes the attention output $\mathbf{C}$ based on a set of queries $\mathbf{Q}$, keys $\mathbf{K}$, and values $\mathbf{V}$: $$ \begin{aligned} \mathbf{C} &= \text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) \\ &= \text{softmax}\left(\frac{\mathbf{Q} {\mathbf{K}}^\top}{\sqrt{d_k}}\right)\mathbf{V}, \end{aligned} $$ where $d_k$ denotes the dimensionality of the key vectors, and the softmax function ensures that the attention scores are normalized to sum to one. The attention mechanism is inherently versatile and can be adapted to various contexts, including self-attention, cross-attention, and multi-head attention.

2.2. Self-Attention in Transformer Models¶

Self-attention, a specialized instantiation of the attention mechanism, enables the model to attend to different positions within the same input sequence. In the context of self-attention, the queries, keys, and values are derived from the same input sequence, and the attention scores are computed based on the compatibility between each query and key pair. Self-attention is permutation-invariant and is adept at capturing long-range dependencies and contextual relationships within the input sequence.

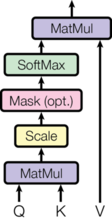
2.3. Scaled Dot-Product Attention¶

The scaled dot-product attention, as proposed by Vaswani et al. in "Attention is All You Need", is a specific form of attention that computes the attention scores based on the dot product between the query and key matrices, scaled by the square root of the key dimensionality: $$ \begin{aligned} \text{attn}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) &= \text{softmax}\left(\frac{\mathbf{Q} {\mathbf{K}}^\top}{\sqrt{d_k}}\right)\mathbf{V}. \end{aligned} $$ The scaling factor $\sqrt{d_k}$ mitigates the potential for large dot products, which could lead to vanishing gradients during training. The scaled dot-product attention is computationally efficient and facilitates parallel processing of the input sequence.

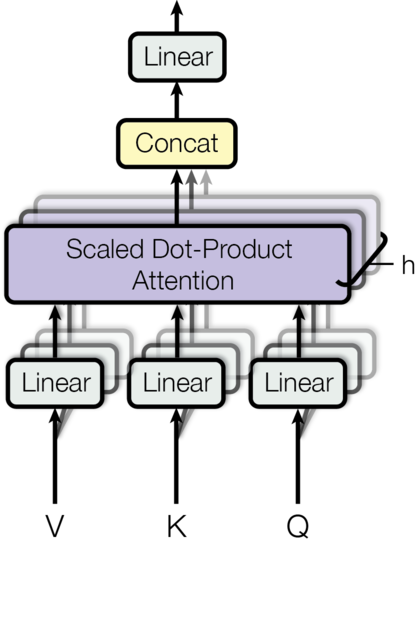
3. Multi-Head Self-Attention¶

The multi-head self-attention mechanism is a salient feature of the Transformer architecture that enhances the model's capacity to capture diverse and nuanced relationships within the input sequence. By employing multiple attention heads, the model is endowed with the ability to attend to different aspects of the input simultaneously, thereby facilitating a more comprehensive and holistic understanding of the input context.

3.1. Multi-Head Mechanism¶

The multi-head self-attention mechanism operates by partitioning the input embeddings into multiple subspaces, each of which is processed by an independent attention head. Each attention head computes the attention output for its respective subspace, and the outputs from all heads are subsequently concatenated and linearly transformed to produce the final multi-head attention output. Mathematically, the multi-head self-attention mechanism can be expressed as follows: $$ \begin{aligned} \text{MultiHeadAttn}(\mathbf{X}_q, \mathbf{X}_k, \mathbf{X}_v) &= [\text{head}_1; \dots; \text{head}_h] \mathbf{W}^o \\ \text{where head}_i &= \text{Attention}(\mathbf{X}_q\mathbf{W}^q_i, \mathbf{X}_k\mathbf{W}^k_i, \mathbf{X}_v\mathbf{W}^v_i), \end{aligned} $$ where $[.;.]$ denotes the concatenation operation, $\mathbf{W}^q_i$, $\mathbf{W}^k_i$, and $\mathbf{W}^v_i$ are weight matrices that map the input embeddings into query, key, and value matrices for the $i$-th attention head, and $\mathbf{W}^o$ is the output linear transformation. The weight matrices are learned during training to optimize the model's performance.

3.2. Independent Attention Outputs¶

The utilization of multiple attention heads engenders a degree of independence in the attention outputs, enabling the model to discern and capture a diverse array of relationships within the input sequence. For instance, one attention head may focus on syntactic relationships, while another may attend to semantic associations. This multiplicity of attention perspectives enhances the model's representational capacity and facilitates the extraction of rich and multifaceted information from the input.

4. Encoder-Decoder Architecture¶

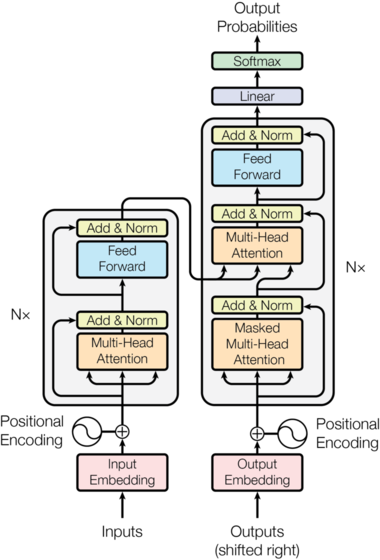
The Transformer model is predicated on an encoder-decoder architecture, which constitutes a fundamental paradigm in neural machine translation (NMT) and sequence-to-sequence modeling. The encoder is responsible for processing the input sequence and generating a contextualized representation, while the decoder leverages this representation to produce the output sequence. The interplay between the encoder and decoder is mediated by attention mechanisms, which enable the model to selectively attend to relevant portions of the input sequence during the decoding process.

4.1. Encoder¶

The encoder of the Transformer model comprises a stack of identical layers, each of which contains two primary submodules: a multi-head self-attention layer and a position-wise fully connected feed-forward network. The multi-head self-attention layer facilitates the extraction of contextual information from the input sequence, while the feed-forward network applies a non-linear transformation to each position independently. Each submodule is augmented with a residual connection and followed by layer normalization, thereby enhancing the model's ability to learn complex and hierarchical patterns. The encoder generates an attention-based representation that encapsulates the salient information from the input sequence, which is subsequently utilized by the decoder.

4.2. Decoder¶

The decoder of the Transformer model mirrors the structure of the encoder, with the addition of a second multi-head attention submodule that attends to the output of the encoder. This cross-attention mechanism enables the decoder to retrieve information from the encoded representation and incorporate it into the generation of the output sequence. The decoder is also equipped with masked self-attention, which prevents positions from attending to subsequent positions in the output sequence, thereby ensuring the autoregressive property of the model. The final output of the decoder is obtained by passing the representation through a linear transformation and softmax activation, yielding a probability distribution over the target vocabulary.

The encoder-decoder architecture of the Transformer model is succinctly captured in the following formula, where $\mathbf{X}$ denotes the input sequence, $\mathbf{Y}$ denotes the output sequence, and $\text{Enc}$ and $\text{Dec}$ represent the encoder and decoder functions, respectively: $$ \begin{aligned} \mathbf{Z} &= \text{Enc}(\mathbf{X}), \\ \mathbf{Y} &= \text{Dec}(\mathbf{Z}). \end{aligned} $$

5. Positional Encoding¶

Positional encoding is a crucial component in transformer models, as it introduces the necessary information about the relative positions of input tokens. This allows the model to capture the sequential nature of language and effectively process the input data. There are various techniques for incorporating positional information, including sinusoidal and learned positional encoding, as well as more recent approaches such as relative position encoding and rotary position embedding.

5.1. Importance of Positional Information¶

In traditional recurrent neural networks (RNNs), the sequential nature of input data is inherently captured through the recurrent connections. However, transformer models lack this inherent sequential processing capability due to their parallelized architecture. To address this limitation, positional encoding is employed to inject positional information into the input embeddings, enabling the model to recognize and leverage the relative positions of input tokens.

5.2. Sinusoidal Positional Encoding¶

Sinusoidal positional encoding is an analytically tractable method for injecting positional information into the input embeddings. It utilizes sinusoidal functions with different wavelengths to create a unique encoding for each position. The encoding formula is as follows:

$$ PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right) $$$$ PE_{(pos, 2i + 1)} = \cos\left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right) $$

Here, $pos$ refers to the position of the token, $i$ corresponds to the dimension of the encoding, and $d_{model}$ denotes the model's dimensionality. The sinusoidal nature of this encoding method allows the model to generalize to unseen positions and offers desirable properties for attention mechanisms.

5.3. Learned Positional Encoding¶

In contrast to sinusoidal positional encoding, learned positional encoding involves training the model to learn the optimal position encodings. During training, the model learns a position-specific embedding matrix, which is added directly to the input token embeddings. This approach allows the model to adapt its positional encoding based on the specificities of the task and data at hand.

5.4. Relative Position Encoding¶

Introduced by Shaw et al. (2018) from Google Brain, relative position encoding is an alternative method that enables the model to focus on the relative positions of tokens instead of their absolute positions. This approach enhances the model's ability to generalize across different input lengths and improves performance on specific tasks, such as machine translation. The encoding is computed using a learnable parameter matrix and a relative position-aware attention mechanism.

5.5. Rotary Position Embedding¶

Rotary position embedding (RoPE) is a recent technique proposed by Su et al. (2021) that allows the model to encode positions in a rotation-equivariant manner. This method involves applying a continuous rotation to the input embeddings based on their positions, which enables the model to capture both local and global contextual information. The RoPE formula is given by:

$$ \begin{aligned} \text{RoPE}(p, d) &= \cos\left(\frac{p}{\text{max\_len}}\frac{2\pi d}{d_{model}}\right) + \sin\left(\frac{p}{\text{max\_len}}\frac{2\pi d}{d_{model}}\right)i \end{aligned} $$

where $p$ denotes the position, $d$ corresponds to the dimension of the encoding, $d_{model}$ represents the model's dimensionality, and $\text{max\_len}$ is the maximum input length.

In conclusion, positional encoding techniques are essential for incorporating positional information within the transformer architecture. Various approaches exist, each offering unique benefits and trade-offs, and ongoing research in this area continues to yield novel and improved methods for encoding position information.

6. Conclusion¶

In this comprehensive analysis of Transformer architecture, we have delved into the intricacies of attention mechanisms, self-attention, multi-head self-attention, and various positional encoding techniques. The transformative impact of Transformer models on natural language processing and machine learning is indisputable, as evidenced by their widespread adoption and numerous advancements.

As we have elucidated, attention mechanisms play a pivotal role in enabling Transformer models to process and analyze vast amounts of data, while self-attention and multi-head self-attention further bolster the model's performance. Moreover, the encoder-decoder architecture serves as the foundation for these models, facilitating the seamless integration of various components.

Positional encoding techniques, such as sinusoidal, learned, relative, and rotary encodings, have emerged as indispensable tools for preserving and conveying positional information in sequences. These techniques enable Transformer models to achieve unparalleled accuracy and efficiency in natural language processing tasks.

Looking forward, we can anticipate further innovations in Transformer architecture, driven by the relentless pursuit of improved performance and novel applications. Research endeavors in both academia and industry are poised to unlock new horizons for these versatile models, paving the way for groundbreaking advancements in natural language understanding and generation.

In conclusion, the Transformer architecture represents a paradigm shift in the field of natural language processing, and its myriad applications continue to revolutionize the way we interact with and understand language. As researchers and practitioners strive to push the boundaries of what is possible, the future of Transformer models is undoubtedly bright, and we eagerly await the next wave of innovations in this dynamic domain.

1. Attention is All You Need
2. Self-Attention with Relative Position Representations
3. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding
4. GPT-2: Language Models are Unsupervised Multitask Learners
5. GPT-3: Language Models are Few-Shot Learners
6. RoBERTa: A Robustly Optimized BERT Pretraining Approach
7. XLNet: Generalized Autoregressive Pretraining for Language Understanding
8. Ernie: Enhanced Representation through kNowledge IntEgration
9. T5: Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer
10. RoPE: Rotary Position Embeddings